Belén González-Gómez (a) y María Isabel Núñez-Peña (a,b)
a Dpto. Psicología Social y Psicología Cuantitativa, Universidad de Barcelona, España
b Institut de Neurociències, Universidad de Barcelona, España.
(cc) CeDec.
Las personas que temen a los números suelen tener menos habilidades matemáticas. ¿Podría estar relacionado con pensamientos intrusivos generados por la ansiedad ante las matemáticas? ¿Se trata, más bien, de una mayor dificultad para procesar las cantidades en la línea numérica mental? ¿Existe alguna huella fisiológica de dicha dificultad? Entender cómo la ansiedad matemática afecta a la realización de operaciones numéricas puede permitir a las instituciones educativas y a la sociedad abordar este frecuente fenómeno de una manera más adecuada y eficiente, evitando las consecuencias negativas que acaba teniendo a largo plazo. En el presente artículo repasamos recientes hallazgos a este respecto.
– Juana, ¿a cuánto tocamos? – dice Miguel, quien de pequeño odiaba las mates.
Es bien sabido que a muchos niños y niñas las clases de “mates” les dan pavor. Y a veces no solo las clases, sino todo lo relacionado con cualquier operación numérica. Generalmente, estos niños acaban teniendo peores notas en matemáticas. Y, a menudo, cuando crecen siguen huyendo de todo lo que huela a números. Por ello, en ciertos grupos de amigos, acaban siendo siempre los mismos los que en el bar calculan a cuánto toca cada uno, ya que algunos, como Miguel, prefieren que de las cuentas se encarguen otros. “Yo es que de números…”.
El fenómeno de sentir emociones negativas al afrontar operaciones matemáticas ha sido llamado por la comunidad científica “ansiedad matemática” (AM) y se han realizado numerosos estudios al respecto. Con el fin de entender de qué manera la AM podría disminuir el rendimiento matemático, Ashcraft y Faust (1994) realizaron un experimento en el que cuatro grupos de personas con distintos niveles de AM (medidos con un cuestionario estandarizado) debían realizar dos tipos de operaciones. Observaron que aquellos con mayores niveles de AM no presentaban mayores dificultades a la hora de realizar operaciones muy sencillas, como sumas de un solo dígito (p.ej., 3 + 5), pero sí lo hacían en tareas algo más complejas, como sumas de dos dígitos (58 + 67). Para explicar este fenómeno, los autores recurrieron a una teoría previa. Esta establece que las reacciones de ansiedad implican la aparición de pensamientos intrusivos (“a mí esto se me da fatal”, “esto es muy difícil”, etc.) que consumen recursos atencionales y mnémicos, restando disponibilidad de los mismos para realizar ciertas tareas mentales (Eysenck y Calvo, 1992). Puesto que las sumas de un solo dígito pueden procesarse de forma automática (recordando el resultado, sin necesidad de llevar a cabo un cálculo), en ellas la AM no afectaría a la tarea, pero al realizar sumas más complejas que requieren atención y memoria (“…y me llevo una”), los pensamientos intrusivos competirían por dichos recursos mentales, empeorando el rendimiento.
Unos años más tarde, Maloney y su equipo observaron, sin embargo, que las personas que sufren AM suelen tardar más en realizar enumeraciones muy sencillas. En concreto, tardaban más en decir cuántos cuadrados había en una imagen cuando el número era igual o superior a cinco (Maloney, Risko, Ansari y Fugelsang, 2010). La hipótesis anterior no era suficiente para explicar esto, ya que procedimientos así no requieren apenas cálculo, así que los autores se plantearon que la AM podría estar asociada a una representación mental de las magnitudes menos precisa.
Los estudios previos en el ámbito de la cognición numérica proponen que las magnitudes se representan mentalmente en una línea numérica interna que nos permite procesar de manera rápida y automática las cantidades (Dehaene y Changeux, 1993). Según esta hipótesis, cada magnitud entera tiene un lugar específico en dicha línea y su representación mental se solapa parcialmente con la de las magnitudes más cercanas (Libertus y Brannon, 2010). Cuanto menor sea el grado de solapamiento entre dos magnitudes, más precisa será la representación simultánea de las mismas y más rápidamente se realizarán procedimientos sencillos, como compararlas (Figura 1).
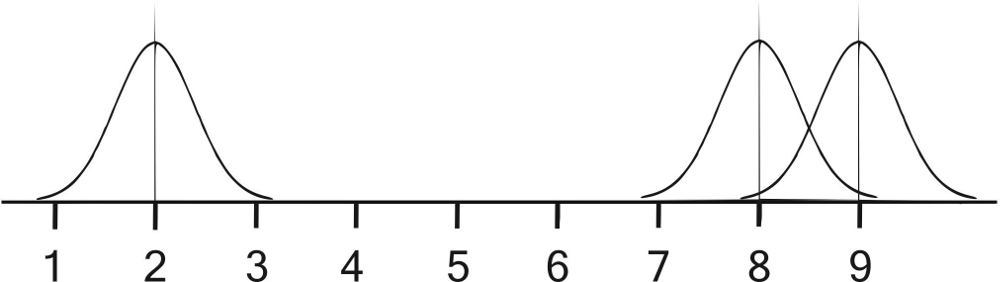
Figura 1.- Línea numérica interna. Según la propuesta de Dehaene y sus colegas (1993), en la línea numérica mental la representación de las magnitudes cercanas se solapa parcialmente. Por ello, tardamos algo más en comparar dos magnitudes cercanas que dos lejanas. Es el llamado “efecto de distancia”.
Esto explicaría por qué cuando dos números son muy cercanos (p.ej., 8 y 9) tardamos más en decir cuál es mayor, que cuando comparamos dos más lejanos (p.ej., 2 y 9). Este fenómeno, que se conoce como “efecto de distancia numérica”, resulta más notorio en unas personas que en otras, ya que el nivel de solapamiento varía entre los individuos, así como a lo largo del desarrollo y en función de la educación matemática recibida.
En este contexto, Maloney, Ansari y Fugelsang (2011) llevaron a cabo otro estudio en el que la mitad de los participantes presentaban baja AM y la otra mitad, alta AM, y se les pedía decir cuál de dos dígitos era mayor. Al analizar la relación entre la distancia de un dígito al otro y el tiempo que tardaban en responder, calculaban el efecto de distancia numérica para cada participante. Comparando los resultados de los dos grupos, observaron que los de alta AM presentaban un efecto de distancia numérica significativamente mayor. Esto es, la diferencia entre lo que tardaban en contestar cuando los dígitos eran próximos y lo que tardaban cuando eran más lejanos resultaba más marcada en el grupo con alta AM. Puesto que previamente se había observado que un mayor efecto de distancia está asociado a un peor rendimiento en la realización de tareas matemáticas, estos autores proponen que la AM estaría, de forma general, asociada a un déficit en el procesamiento mental de las magnitudes, déficit que a su vez comprometería la realización de operaciones más complejas, al ralentizar las tareas sencillas subyacentes.
Algo después, Núñez-Peña y Suárez-Pellicioni (2014) profundizaron en el asunto, estudiando adicionalmente los patrones neurofisiológicos cerebrales, mediante un análisis de potenciales evocados. Estos muestran las fluctuaciones en el potencial eléctrico que pueden detectarse en el cuero cabelludo (mediante un electroencefalograma) y que aparecen ligadas a una función cerebral. En tareas de comparación numérica, se había observado previamente un pico de voltaje positivo, registrado en la zona frontocentral de la cabeza en torno a 200 milisegundos después de presentar el par de dígitos (P200), que aumentaba cuanto menor era la distancia entre los mismos. En este estudio, las autoras descubrieron que tal huella fisiológica del efecto de distancia era significativamente mayor en el grupo con alta AM (Figura 2; para estudios relacionados, véase Suárez Pellicioni, Núñez-Peña y Colomé, 2014).
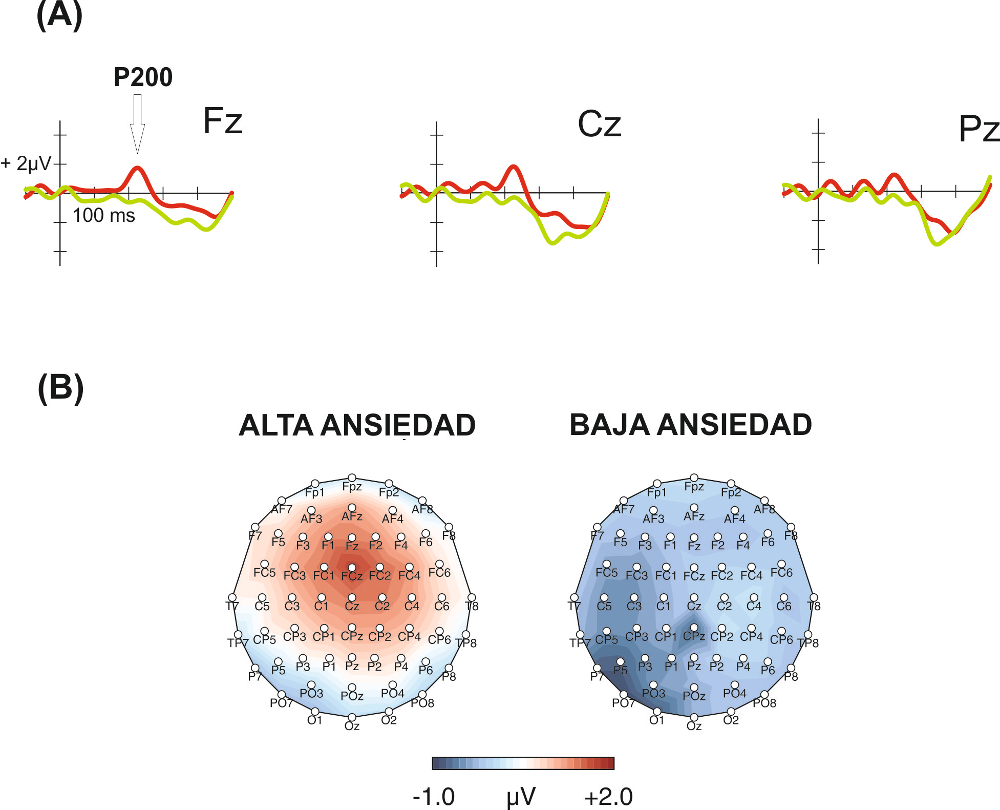
Figura 2.- Efecto de distancia en P200. A) Fluctuaciones de voltaje medidas por un electrodo frontal (Fz), uno central (Cz) y uno parietal (Pz), después de presentar el par de dígitos en la tarea de comparación numérica. Las líneas recogen la diferencia entre el voltaje medio registrado cuando los dígitos son cercanos y el registrado cuando son más lejanos (efecto de distancia) en el grupo con alta ansiedad matemática (rojo) y con baja ansiedad matemática (verde). Se aprecian visualmente las diferencias grupales en el pico que aparece a los 200 milisegundos (P200), huella fisiológica que acompaña al efecto de distancia, haciéndose patente en el grupo con alta ansiedad. B) Distribución espacial de este efecto fisiológico de distancia (rojo cuando es mayor) en el intervalo de 200-250 ms después de la presentación de los dígitos, en ambos grupos. Puede observarse que tal efecto se da en las personas con alta ansiedad matemática en electrodos frontocentrales.
Teniendo en cuenta estos descubrimientos, es probable que la explicación más plausible a las dificultades que las personas con AM suelen presentar en cuanto a rendimiento matemático consista en una conjugación de las dos propuestas. Así, estas personas dispondrían de una representación mental menos precisa de las magnitudes que, combinada con la distracción de los pensamientos intrusivos causados por la ansiedad, ralentizaría el procesamiento requerido para ciertas tareas matemáticas.
Estos conocimientos, junto con los relativos a los factores que promueven el desarrollo de la ansiedad a las matemáticas (experiencias negativas en el aula, estereotipos de género, etc.), deberían llevarnos a diseñar programas de intervención y entrenamiento básico, así como mejores estrategias educativas para prevenir y abordar este tipo de ansiedad desde la sociedad y, sobre todo, desde las escuelas. Así conseguiremos que futuros “Migueles” calculen, sin miedo, a cuánto tocan.
Referencias
Ashcraft, M. H., & Faust, M. W. (1994). Mathematics anxiety and mental arithmetic performance: An exploratory investigation. Cognition and Emotion, 8, 97–125.
Dehaene, S., & Changeux, J. P. (1993). Development of elementary numerical abilities: A neuronal model. Journal of Cognitive Neuroscience, 5, 390–407.
Eysenck, M. W., & Calvo, M. G. (1992). Anxiety and performance: The processing efficiency theory. Cognition & Emotion, 6, 409–434.
Libertus, M. E., & Brannon, E. M. (2010). Stable individual differences in number discrimination in infancy. Developmental Science, 13, 900–906.
Maloney, E. A., Ansari, D. y Fugelsang, J. A. (2011). The effect of mathematics anxiety on the processing of numerical magnitude. Quarterly Journal of Experimental Psychology, 64, 10-16.
Maloney, E. A., Risko, E. F, Ansari, D., & Fugelsang, J. (2010). Mathematics anxiety affects counting but not subitizing during visual enumeration. Cognition, 114, 293–297.
Núñez-Peña, M. I., & Suárez-Pellicioni, M. (2014). Less precise representation of numerical magnitude in high math-anxious individuals: An ERP study of the size and distance effects. Biological Psychology, 103, 176-183.
Manuscrito recibido el 26 de septiembre de 2017.
Aceptado el 8 de enero de 2017.

